(Note updated 1/30/2024 – This article, more than any other, gets non-stop daily traffic on my blog from around the country as well as internationally. As of 1/30/2024, it has been viewed 28,283 times. Parents, students (and even teachers as you can see in the Comments section following the article below) are looking for information about CPM beyond that provided by the publisher, often when students start struggling with the math program.
Although this article was originally composed in August 2017, its contents remain completely relevant today.
I’d appreciate it if readers would leave a comment below about what prompted them to search for and read this article. You might also want to name your school district in case others in your locale are in the same situation. There is strength in numbers.
Thank you! I am also open to suggestions for additions or clarifications to the material contained herein. You can contact me here.
Finally I would like to call your attention to probably the most important article that I have written for this blog: Raising our Children – American Society Reflects our Values and Choices. Other top-ranked articles are listed on the main home page.)
8/28/2017 – This article was prompted by the comments of a parent to my last blog article. Those comments were made on Nextdoor, not on this site. (The Nextdoor link will only work for local residents who have Nextdoor accounts.)
Referring to the new math curriculum “pathways” or course sequences from 6th through 8th grades, the parent said:
I would add that these new pathways and CPM curriculum (2014) were unveiled with promises that they would provide a deeper and more comprehensive math program. My observation is that this curriculum is more confusing and less comprehensive. I have two daughters who enthusiastically take Math at RSM and who can explain how little material is covered in CPM textbooks and what a superficial foundation they provide in math.
RSM is “The Russian School of Math,” a private organization with an office in San Mateo and many other locations across the U.S.
The CPM (College Preparatory Math, www.cpm.org) mathematics textbook series is used in many classes at Aragon High School (as well as some other SMUHSD schools such as Hillsdale HS). According to Superintendent Dr. Joan Rosas, it was also adopted by SMFCSD middle schools to align their curriculum with the high school curriculum.
I first used this math series when I taught 9th and 10th graders at George Washington High School in San Francisco, and have tutored many local students who are using these textbooks in class. I should also note that the unfortunate CPM precalculus textbook trial two years ago at Aragon was the motivation for my starting to blog, first on Nextdoor.com, and then at this site.
Although many teachers will say that CPM is the best mathematics series that they have used, I have very mixed opinions about it and am NOT an unabashed fan of the program as I will detail below.
A Google search on “opinions on CPM math” may interest you and will display the experiences of many other communities.
The CPM Math Program
CPM spans middle school to high school math, previously stopping at precalculus, but lately including Calculus AB and BC textbooks. The program strongly encourages group work over individual study.
Students are typically placed in groups of four in their classroom and are given defined roles within their group: “Resource Manager,” “Facilitator,” “Recorder/Reporter,” and “Task Manager” (see the beginning of any CPM textbook for details if you are interested in what these roles entail).
CPM literature frequently mentions that in the “real world” people work in teams, and therefore CPM aims to teach and facilitate collaborative learning. Many teachers have told me that students are more engaged with the CPM math curriculum than with any other series that they have tried. Students have active discussions about the material and work on group problems in class versus passively listening to lectures, taking notes, and only working actively when they do homework alone after school.
As long as the program works in this manner this is definitely a strong positive in its favor. Mathematics is definitely learned by working problems actively rather than watching a teacher do them on the board. It is also a major plus to work problems in class, when others are around to offer a helping hand, instead of finding later, when starting the homework at home alone, that one didn’t understand the material.
A typical CPM lesson works as follows. Each textbook section begins with a series of guided questions that lead students to discover a new math concept if they answer the questions correctly and in order. Often these guided questions are quite clever and well-designed. The books do not simply explain a math idea and and then provide worked examples to imitate, as do traditional math texts. Students work with their groups to solve the set of problems and learn the lesson that the section intends to teach.
Teachers are supposed to move around the class from group to group, answering questions from each group and making sure that students are on task. Lecturing is kept to a minimum. This is in agreement with the “learning by doing” philosophy. Current teaching practice tends to denigrate lecturing, calling a lecturer a “sage on the stage,” with the implication that lecturing stokes the ego of the teacher instead of really instructing the student.
As I have found with many ideas in education, such theories work great when one has motivated students who actually do the work. If the student groups are well-structured, the better students help those in their group who struggle with math, and everyone benefits. The good students benefit because, paradoxically, there is no better way to learn a subject than to teach it. The less mathematically-inclined students get help from their peers, which is often less intimidating than asking a question from the teacher.
However, if a teacher has a class of mainly lower level students who have not done well in math previously, the CPM method can become problematic. Putting pre-teens or teens who “hate math” into groups results in a major “classroom management” challenge for a teacher. The group conversation is often on any popular teenage topic other than mathematics when the teacher is not watching!
Again, if a group is able to finish the guided questions, then they learn the lesson for the day. In a poorer class, however, the teacher often has to answer the same questions repeatedly for each group and may eventually decide to stop the class and lecture for a while on the topic.
During the one-year CPM precalculus trial at Aragon, two school years back, one of the teachers tended to lecture at the beginning of each class. That teacher’s students were appreciative of this lecture effort while those in classes where the teachers followed the standard self-discovery prescription were often frustrated. In fact I had one student, who was totally upset with a teacher’s “hands-off” approach, comment to me, “Don’t they get paid to teach??!!??”
CPM basically is a set of pre-made math lessons which alleviates a lot of lesson planning for teachers. A motivated teacher can use these lessons as PART of a good curriculum as I will explain further below. Unfortunately this also means that a burned out teacher can use the CPM program as an excuse to coast. The lessons are spelled out in the book, the students are supposed to do the work themselves, so “get in your groups, open your book to section X, and do problems Y to Z” is the very minimal teaching effort required.
Typically, the group problems in the first part of each section take up most, if not all, of a class period. The second part of each textbook section is a set of problems (with no additional explanatory material) entitled “Review and Preview.” These “review” problems are typically assigned for homework. Hints for the homework problems are online at the CPM website, and Aragon teachers frequently post answers online. The “review” problems include some additional practice on the ideas just learned in the guided questions section, but also include review problems from earlier textbook sections. This practice of frequently returning to older topics in each new section is called “spiraling.”
[Aside: The spiraling concept can also come into play on CPM chapter tests, i.e., the chapter 4 test will include problems not only from chapter 4, but also from chapters 1, 2, and/or 3. This can turn a chapter test into what is basically a mid-term or final exam. On the plus side, the constant cycling back can really reinforce the material. On the minus side, students can feel really stressed as the tests can cover much more material than traditional chapter tests.]
The “Review and Preview” homework section may also include “thought” problems (called “preview” problems) on topics that students have not even encountered yet. The purpose of such questions is probably to see if a student can discover the solution to a completely new, challenging problem on his/her own. Unfortunately, “preview” questions tend to confuse all but the very best students.
Critique of CPM
Having now described how the “Review and Preview” section works, I must next note its most serious drawback. I have seen many instances where the “Review and Preview” section offers only minimal additional homework practice on the lesson just learned and then “spirals” back to problems from earlier sections picked in a rather random fashion.
Too often I have tutored students who are just beginning to master a new concept when the homework diverts them back to earlier topics without cementing the knowledge just learned. I then have to use other sources or make up my own problems to help the student.
Traditional texts give a far greater number of practice problems than CPM. They usually have solutions readily available to odd-numbered problems and have worked examples, both of which allow a motivated student to do extra work if they still don’t understand a concept.
This is much harder to do using the CPM series. In my experience a teacher who decides to use CPM needs to give students supplemental practice problems. If one has to find this extra material, then one needs to be convinced that the CPM guided questions are so good that it is worth this extra trouble, instead of simply using a different textbook.
One must also strongly believe in the value of the self-discovery process. “Self-discovery” as a teaching method is not universally accepted, and I address the issue of self-discovery versus fully guided instruction further below.
In summary, the biggest problems with CPM are the lack of explanations, worked example problems in the textbooks, and insufficient practice problems. The first two omissions are by design because each group is supposed to discover the concepts through the guided questions. Worked examples would circumvent this process.
However, if a group does not “get” the topic and fails to complete the guided problems in class, they are left with nothing to explain how they should do the homework! Essentially the student has a textbook with only questions and little or no explanations. This is a significant problem in classes with weaker math students and with students who are absent from class. They have nothing to refer to at home unless the teacher puts additional material on the Web. However, this means the students have to navigate to other sources instead of just being able to use their textbook.
The CPM books do have small boxed highlight sections called “Math Notes,” usually in sections of the book beyond the section being studied that day, that try to summarize the important points. These sections are very concise and also do not contain worked examples as do traditional math texts.
Another learning problem can arise because many schools use the cheaper paperback version of the CPM books which are split into two volumes. The index is in the second of two books, and the student may not have book 2 during the first part of the year. Only the hardback version is a single volume. Lack of an index makes it difficult to look up particular concepts when one is “stuck.”
Critique of the Self-discovery Methodology
Finally, and the most important learning issue in my opinion, the self-discovery method tends to work better on easier concepts such as Algebra 1. As one moves up the math hierarchy and ideas become more complex, self-discovery becomes increasingly time-consuming and inefficient.
I think this was a major reason why the CPM precalculus experiment at Aragon failed, and why at least one of the teachers had to revert to lecturing.
In fact I presented the teachers at Aragon with an article from an American Federation of Teachers journal critiquing “self-discovery” methods when I met with them early in the 2014-2015. I warned them early in the school year, first by emails and then in a face-to-face meeting with math department staff, the principal, and a vice-principal, that the CPM experiment was in grave danger of running off the rails. I believe the principal had evidence of this too, which is one reason why the meeting took place. The precalculus students that I tutored that year were clearly struggling significantly more than in years past when a traditional textbook was used.
The article I gave Aragon staff was in the Spring 2012 issue of American Educator, vol. 36, no. 1, and it was a through review of numerous educational research studies including academic references. The article concluded:
Research has provided overwhelming evidence that, for everyone but experts, partial guidance during instruction is significantly less effective than full guidance.
To date, I have no indication that anyone at the school ever took the time to read this article unfortunately. If the article’s conclusion is true (I think it is, and the research in this article has the great advantage of correlating closely with common sense unlike many teaching fads), this is a damning condemnation of the CPM methodology.
The fact that CPM now has textbooks for Calculus AB and BC makes me shudder. This would raise self-discovery to the highest level of complexity in high school math. I would be extremely concerned if any of the SMUHSD schools adopted those books.
Research Supporting CPM
Having discussed the CPM methodology and its pros and cons, one might still wonder what kind of research does CPM tout to promote their program? If one takes the time to navigate through the cpm.org website, one can find a section detailing research studies behind the CPM program.
Much of the research is older, probably in part because the standardized STAR test base was discontinued with the adoption of Common Core. However it is interesting to look at one of the later studies from 2013 in 8th grade and high school.
The methodology of this study is very flawed, however, because it appears to only take the results of school districts that CPM knew used their books and compare them to statewide averages. There is no controlling for differences in, e.g., demographics between districts that adopted CPM and the state as a whole. Nevertheless, there is no indication that schools using the CPM series did any better (or worse) than the STAR test state averages in Algebra 1 and Geometry and only slightly better in Algebra 2.
This might not seem too bad until one realizes that our local schools have always prided themselves on scoring significantly ABOVE the state average! Why would they want to adopt a series that only delivers average state test scores, particularly when we know how pathetic state math scores have been??
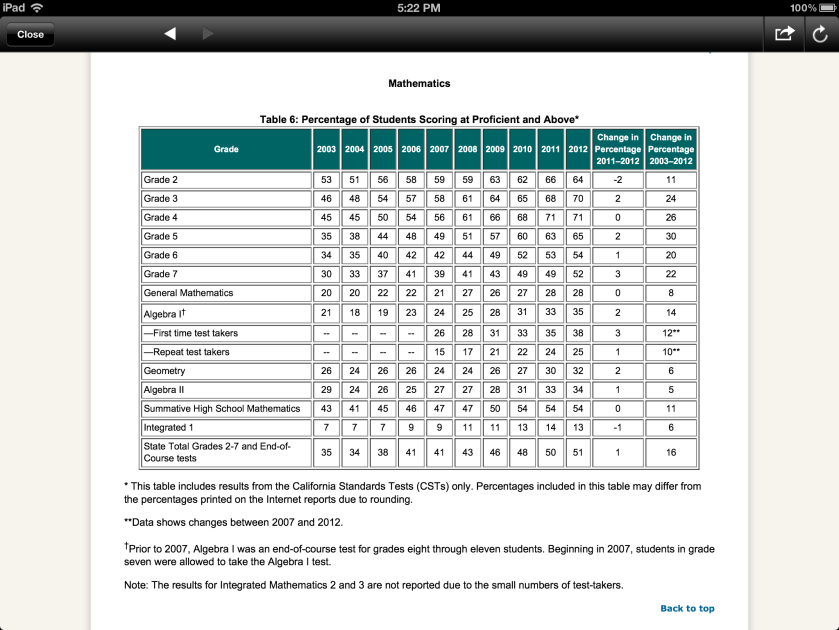
The illustration below shows California STAR math scores (% scoring proficient or above) from Grade 2 up through Algebra 2 for years up through 2012 before the state terminated this test in favor of newer Common Core testing. As one can see, there was a downward slide in math scores from 4th grade through high school in 2012.
Passing rates of 35%, 32%, and 34% are not benchmarks that I would want to use for marketing any product that I developed!!! Why would one adopt a program if this is the research used to promote it??
In fact, I learned from an administrator that CPM was tried in the SMUHSD years ago, long before Common Core was a glimmer in anyone’s eye, and was abandoned by all high schools except Hillsdale! The group work encouraged by Common Core appears to be resurrecting it from the dead.
Postscript
One final aside which I did not mention earlier as it is a lesser, but persistent, irritant for many parents: students in CPM classes also engage in a practice called “group tests.” All four students in a group work collaboratively on a test. At the end of the period, the teacher randomly picks one of the group’s four test papers, grades it later, and then assigns that grade to everyone in the group.
The first time this happens during the school year, some of the groups will have a paper selected from the weakest student in the group, and everyone in that group might end up with a bad grade. During subsequent group tests, the better students in the group will frantically check that everyone’s test papers have the same answers, so that they do not “get screwed over” a second time. Parents tend to shake their heads incredulously when they learn about this practice, and I can’t blame them.
However, I don’t see that this has to be an essential part of a CPM class and could be eliminated if a teacher so desired. Of course, this would require grading four times as many tests… However, I always thought that the purpose of a test was to assess what a student knew, not what his/her group can gin up and copy in a hurry…
NOTE: If you found this article to be of interest, you may also want to read Why Can’t We Teach Mathematics Properly?
Please post your comments following this article below. You must scroll all the way down to the “Leave a Reply” box to reply to the article directly or click the Reply link following a particular comment to respond primarily to that comment.
The WordPress software that runs this site requires that you enter an email address to comment, but your address is not checked for validity nor displayed, and I do not collect or use this information. Also, you will not receive emailed comments on the article from other people unless you check a box in the form to request this.
Thanks as always for your participation!

I stopped offering studies because you have already said that the NAEP is not worthy of our attention and you also rejected one (or two?) studies because of their sample size. I dropped that line of discussion because I got the strong feeling it wouldn’t matter. You offer no research to the contrary – only personal experiences. I thought that was the basis of our continued discussion, and so followed it. I looked up a number of articles that you might find helpful – all research based. Since this website doesn’t allow attachments to posts, all I can do is offer you the titles. At your request I will send pdfs to you via email. They are:
“How Kids are Performing: A Snapshot of K-12 Acdemic Performance and Growth” in Special Report Series, 2021-2022 Edition, Renaissance Learning.
“Reforming Mathematics Classroom Pedagogy: Evidence-Based Findings and Recommendations for the Developmental Math Classroom”, Michele Hodara, Feb 2011 CCRC Working Paper No. 27, Teachers College Research Center.
“The Implementation and Impact of Evidence-Based Mathematics Reforms in High-Poverty Middle Schools: A Multi-Site, Multi-Year Study” Robert Balfanz, D MacIver and V Byrnes, Journal for Research into Mathematics Education 2006, Vol. 37, No. 1, 33-64.
“Improving Students’ College Math Readiness: A Review of the Evidence on Postsecondary Interventions and Reforms” Michele Hodara CCRC, Teachers Colege, July 2013.
“Cooperative Learning, Success for All, and Evidence-Based Reform in Education”, Robert Slavin, Education et didactique, 2-2 Septembre 2008, p. 149-157.
Research on Reform in Mathematics Education, 1993-2000″ John Ross, D McDougall and A Hogaboam-Gray, The Alberta Journal of Educational Research, Vol. XLVIII, No. 2, Summer 2002, 122-138.
I apologize I didn’t spend the time to find more or necessarily the most convincing. I went to Google Scholar and gave you the first few listed there. If you want to see more, you can do the same. You could probably find a few that support your position – though not many that are research-based.
About the overall gist of your complaint: please don’t mistake diplomacy for failure to recognize an argument. I simply can’t respond to everything and remain within the bounds of a productive back and forth between us. I understand, from your (apparent) growing agitation with this exchange, that you are feeling that strain as well.
The various facts cited are perhaps not pertinent to what you perceive as your argument, but they were cited as a reminder that what you are perceiving as a current or seven-year fashion in Math Ed (particularly in California) is in fact EXACTLY that evolution that you seek. I think you aren’t recognizing it for what it is – though I can’t say why.
LikeLike
From the previous comment: “I stopped offering studies because you have already said that the NAEP is not worthy of our attention and you also rejected one (or two?) studies because of their sample size.”
Richard, did you read my last response? I said, “We previously discussed *** PISA ***, i.e., international, test scores, *** not NAEP ***, national test scores, so once again you are misrepresenting my position to score totally bogus debating points.” I then elaborated on that point in the paragraph that followed this quote.
I rejected the study from Mauritius as it was based on only interviews with 8 students at a school there. Specifically I said, “The Mauritius study was unfortunately a great example of worthless “research” as it consisted of a sample size of **8** students. As I have said elsewhere ( https://eduissues.com/2018/01/29/never-believe-educational-experts-or-me/ ), too much of educational research not only has serious methodological flaws but often also has financial conflicts of interest (e.g., publisher sponsorship).”
To elaborate, it is ridiculous to draw any conclusions on adopting a curriculum for widespread use in the U.S. based on interviews with 8 students in Mauritius. Your earlier response (16 days ago) was “I appreciate your criticism of several studies based on sample size. That might be a problem – but isn’t by itself a solid criticism. There is an accepted protocol for small sample studies and these are accepted throughout the sciences daily. A small sample size cannot by itself be the support for a declaration of “worthless” for a study.”
A) I only mentioned the Mauritius study but you keep saying that I rejected multiple studies based on sample size.
B) Yes, there are statistical methods for small samples, but this does not make it a good scientific practice to use small samples when adopting a curriculum that can impact literally thousands of students and potentially result in a major set back in their education. We had a disastrous implementation of a spiraling curriculum (Everyday Mathematics) in our local K-8 district which supposedly was well-researched (over 90 studies – the *number* apparently convinced local educators that it must be good!). When the Department of Education reviewed the research they rejected all of the studies as being statistically invalid, though they did allow that *one* of the 90+ studies at least pointed in the right direction. See https://eduissuescom.files.wordpress.com/2022/06/13_everyday_mathematics.pdf and https://eduissues.com/2018/03/01/why-cant-we-teach-mathematics-properly/.
Thank you for providing additional references (I will look at them when I have time), but it is not clear that you are still understanding my data request despite my stating it multiple times. The CPM organization attempted to show that districts adopting their curriculum improved math STAR test scores about a decade ago. The best that they were able to come up with allowed them to say that their results were comparable or slightly ahead of in some cases to districts that were not using CPM. Their STAR results were *far worse* than those of our local high school district as I mentioned in my original CPM article and thus their “research” gave little concrete reason to adopt their program. PLEASE NOTE that the focus here and in my original article is on *CPM* specifically and NOT the concept of spiraling in the abstract
You earlier provided me references about the benefits of self-discovery and spiraling. What I keep asking for is a quantitative study with a significant number of students (and hopefully multiple districts), that clearly shows that districts adopting **CPM** improve overall math test scores. CPM had a call for research proposals on their website for quite some time as I indicated in earlier comments, and I never saw anything come of it. It is not clear to me that any of the new references you cite are of that nature, but I will check anyway.
You will note that I take the time above to go back and read and quote both what you and I have written previously. By contrast, your responses seem to rely on a hazy memory of our earlier exchanges, and I keep pointing out your misrepresentations of my positions in them.
I try hard to be fair to all sides in my moderation of this website but if your replies continue to be of this haphazard nature, I am going to cease posting them as it is becoming a very clear waste off my time to attempt to maintain a conversation here. You ignore much of what I say in the interest of scoring debating points to support your side.
LikeLike
Clearly you are at your limit, David. I’m sorry about that. The research that is based on CPM alone probably doesn’t exist outside of the Districts that have collected it on their students. I’m sure you realize that research that supports the methods of CPM, which I’ve demonstrated is numerable, ought to be enough. If you choose to allow in your discussion only that very narrow slice of research possibility, AND reject small studies, I don’t think you’ll ever be satisfied. I wonder if you’ve ever seen ANY curriculum so supported, except by in-house studies (which we should all question, at any rate?) You’re right about the decreasing marginal utility of this conversation, though. Be at peace, David.
LikeLike
When a major medical question requires attention in this country, the National Institutes of Health, sometimes along with other collaborating government agencies, will marshal resources from Congress and put out a Request for Proposals to the biological research community. Not only medical researchers but statisticians will be involved, and the research is peer-reviewed. This method has led to many benefits in pharmaceuticals and biotech.
We have the U.S. Department of Education along with numerous college/university departments of education which all have a fair number of Ph.D.’s. If we really are concerned about education and the future of our students in this country, when a curriculum comes along that is promoted nationally like Everyday Mathematics or CPM, instead of letting publisher sales reps fan out and let every school district in the country do its own evaluation with widely differing resources, why doesn’t the Department of Education organize more comprehensive and more controlled studies of these materials??
I am simply asking if you have seen any such studies. It sounds like the answer is no.
The Department of Education had its “What Works” database which I mentioned in my articles about Everyday Mathematics, but when I looked at Everyday Math, it looks like all that the DOE did was comment after the fact on studies done by others and played no oversight role at the start. I showed to some local teachers my startling findings in the DOE database that contradicted McGraw-Hill sales rep claims, but those teachers did not seem to be aware of the studies cataloged by DOE nor were they aware of the database itself, even though they participated in a local evaluation of the textbook series.
We currently accept a broken method of textbook evaluation where the wheel is reinvented locally with differing results across the entire U.S. I did research in biophysics and cell biology and published numerous papers in prestigious peer-reviewed journals. I did not take graduate classes in education, but I rarely come away impressed with the education research papers that I have read. It seems to me that the DOE could do a much better job in research coordination/funding but I would not be surprised if political conservatives might try to block such a move.
To sum up, when I wrote my article about CPM, I acknowledged that its methods worked for some of the lower level math classes like Algebra 1, but I questioned its applicability to higher level math courses where the amount of material to be covered is greater and more complicated. Locally the high school CPM precalculus trial failed dismally. I also questioned CPM’s effectiveness in classes with kids who were far behind in math and who do not have much motivation for self-discovery methods. I never denied that spiraling has advantages, but there is an obvious trade-off when one spends time reviewing older material and thus can not cover as much new material. I did question specifically *CPM’s* effectiveness in implementing spiraling, saying several times that the textbooks do NOT provide sufficient initial practice problems.
As one progresses past algebra, students self-select to take more advanced math classes, and the pace has to increase if mathematicians are ever to get to the frontier. There is far less need at that point to use techniques to try and educate the entire general populace, many of whom do not go beyond algebra. At some point a student learns to tackle mathematics through their own efforts or leaves the field. The same is true in any other advanced discipline.
Finally, I am also not surprised by any means with the learning loss in traditional classes; anyone who ever was awake as a student experiences that personally after a summer break or when reviewing for a final. One does not need math teacher training to come to this realization. Despite this “flaw” in traditional learning, the U.S. still managed somehow to become the technological leader of the world. Whether we will remain there is uncertain, and you are correct that a lot of changes in math education arose from concerns about our eroding competitiveness.
Whether this competitiveness problem be resolved by curriculum changes like mathematics spiraling or whether this reflects the consequences of other more serious tears in the fabric of our society (which I think is more likely) can be debated endlessly. But I agree with you that we should bring this exchange to a close. Best of luck in your teaching endeavors.
LikeLike
Hello. Thank you for writing this article. I work at a private school and we’re considering CPM texts for Geometry, Algebra 2, and Precalculus. I am in favor of collaborative learning, problem-based learning, spiraling, and many of the other methods employed by the curriculum, but I feel that the actual implementation of these methods by CPM leaves much to be desired. I feel that many of the problems lack depth, and relevance, and are not really that different than ordinary textbook exercises. Why is this texbook better than, for example, a traditional textbook that contains exposition, examples, practice exercises, AND (more) interesting problems?
I understand that the methods that CPM is built upon are supported by research, but I would like to see validation studies of the actual CPM textbooks and curriculum. Just because the methods utilized are supported by evidence doesn’t imply that the curricula or textbooks are actually effective. I can certainly entertain the possibility that these methods work, but the textbooks and resources are not as effective as a traditional textbook paired with collaborative problem based teaching practices.
Are you aware of any actual evidence that CPM is more or less effective than more traditional approaches in similar learning environments?
LikeLike
You can look at the CPM research base that I cite in the article. I found it highly lacking. Many people commented on the curriculum in the Comments section following the article. I hope you looked at their remarks too. You will find comments from both supporters and opponents of CPM.
LikeLike
Hey David,
Thanks for your reply. We ended up choosing to use the CPM program for Alg 2 and I think my students and I have had overwhelmingly positive experiences with it. I’m happy to discuss my experiences with you.
LikeLike
Hi Andrew. I am glad your Algebra 2 implementation went well and would be happy to either post your comments about it here or you can contact me privately via the Contact page. You might want to look at my response to “Heresolong” (just posted, so near the end of the lengthy comments section as of 3/13/2024) which is also very relevant to your concerns.
LikeLike
There is so much that I can say about CPM. It is a textbook and all textbooks are not curriculum and do not make excellent instruction in themselves, especially for all students. Since I have been teaching, my students have sat in groups and have worked together. I have used lesson study lessons either created by myself or modified from master teacher lessons from Japan as well as other group activities. I have modified my strategies to meet English as a Second Language (ESL) learner with a wide range of activities that build language and then connect to the mathematics. These include SIOP methods, Frayer models, graphic organizers, and hands on activities, etc. Each student is unique and have different ways of learning and comprehending instruction. CPM is a highly demanding in terms of its literacy, numeracy, and critical thinking skills, in addition, student must have the required back ground knowledge to be successful.
I have to agree with Prof Kristofferson. I have taught CPM for two years now in Detroit Public Schools and it was difficult. In the past my group activities always allowed lower groups of students to be able to access the activities and be successful. I think CPM should be modified to include some direct instruction. Many of the sections could be combined, and the assignments should be less random and should connect to what we are doing so that students can make connections. Thoughtful spiraling is important, random spirlaling, not so much. The textbook should be disposable so that students can use close and critical reading strategies to be more effective readers, since reading levels from district to district and student to students vary.
LikeLike
Thanks for your comments, Marianne!
LikeLike
I haven’t had a chance to read all the comments, having just found this article but thought I’d address a couple things I’ve experienced as a teacher who uses and likes this curriculum.
1) It does require heavy teacher involvement and CPM makes this quite clear. The training they make available emphasizes this. No student is expected to just “figure it out”. My typical class period involves me introducing the topic, emphasizing what the students should be looking for through Period Learning Targets, and then running laps where I engage in questioning strategies to help students move in the right direction. As time progresses I hear students asking each other the same questions that I asked earlier in the year, resulting in more successful progress without my intervention.
2) I liked the Pre-calculus as I thought it did an outstanding job of introducing the key concepts of Calculus but without all the notation and labels. Students leaving the CPM PC were very good at understanding the concepts of limits and slopes. The main failing of the curriculum that I saw is that it didn’t spend enough time working through more complicated algebraic problems and so they were weak in this area when they arrived in Calculus.
3) I agree that there isn’t enough practice in CPM. We routinely add problem worksheets to emphasize a particular solving strategy.
4) I do not believe, however, that the lack of significant immediate practice in many topics is a major concern, due to the spiraling nature of the curriculum Ideas are often introduced in a very basic manner, then come up again later with more complexity. I have seen significant progress made by students who didn’t quite get it the first time but by the time it shows up again they have the basic idea down pretty well.
5) The idea that a test should only assess what we just taught/learned is inimical to actual learning, imo. Teaching in a standard lecture based system we would have to do massive review prior to the “final”. We don’t even give a final in our CPM classes, but just keep retesting ideas that have come up earlier, and include them on review worksheets, etc.
6) Finally, the team test is not the only assessment and, in my classrooms, is more of a review worksheet. Yes, everyone gets a grade together but it is a Classwork Grade, not a test grade, and is really a formative assessment. It helps the students work together, it ensures that they are checking each others’ work, and it encourages cooperation and effort, while letting students self assess the topics that they personally didn’t know and had to rely on others for.
Anyway, there’s a few thoughts.
LikeLike
Thanks for your comments, John. It sounds like you are a very involved and conscientious teacher, so kudos for that. Dedication counts for a lot in any successful implementation.
There are scores of comments on this article which has now been accessed almost 28,000 times. Comments by teachers run the gamut, with some loving CPM and others steadfast against it. My experience has been more positive in the lower level math classes than in the higher level ones, but their Calculus books have not been used in our local district (fortunately, IMHO). As I stated previously the experiment with their pre-calculus program was not successful here and was dropped after a year (though the “guinea pigs” in that experiment suffered from learning deficits afterwards as I described).
LikeLike
As a special education teacher for 7th and 8th grade students, I find CPM to widen the gap between students with disabilities and those without. I love the hands on manipulatives used, but other than that, I am not impressed. The textbooks contain a large amount of writing written at a 900 Lexile level or higher. So now, students who did not struggle with math and just receive services for reading, struggle due to the paragraphs and paragraphs of text they have to read on a daily basis. Students who have Autism that struggle socially, typically have a very hard time participating in the groups. Then they get docked for not contributing to the group. Students who struggle with math are afraid to hold their group up so they just copy down answers of other members. If they do try to ask questions they usually get a snarky comment back from a peer accusing them of not paying attention or an eye roll shot at them for keeping them from getting done faster. There are a few students who will help group members, but those students are few and far between. Even when groups are using appropriate voice volume, it is loud and distracting in the room. This makes it near impossible for my students with AD/HD to focus. Any student who is deaf/hard of hearing or has an Auditory Processing Disorder is missing most of what is being said. We are having to accommodate way more than before and having to pull students for service at an alarming rate because of how the class is designed. This is all with amazing math teachers at our school and with myself in the classroom supporting.
LikeLiked by 1 person
Thank you very much for your comments, Mikaela.
LikeLike
After reading your article and browsing through some of the comments, thought I’d throw in my own anecdotal observations.
1) “one student, … comment to me, “Don’t they get paid to teach??!!??”
I would suggest that a student’s comment on what constitutes teaching is somewhat irrelevant since they have no idea. Teaching does not necessarily mean “telling students how to do things”. Just read up on the Socratic Method.
2) I would consider myself a good teacher. I’ve been using CPM for 17 years now and I love the level of interaction and communication within the groups. It doesn’t happen automatically. We start with Algebra and we teach those skills. Additionally I spend my time circulating amongst the groups. I ask questions and sometimes answer them, but mostly socratically, by asking more questions. It does frustrate students at first but I also explain clearly to them why we are doing it, so that they can get better at figuring out what questions to ask. I have even overheard groups who were stuck and waiting for me to get to them say “if we can figure out what questions Mr. Armerding will ask us, maybe we can figure it out ourselves.” By the time I got to them, they had figured it out.
3) This is not a good curriculum to start in a higher level class. The math is complicated and they don’t know how to work together or think about the process. Starting in Algebra, however, allows them to develop those skills which are then automatic by the time they get to Geometry and Algebra 2 (especially the latter which is much more conceptually difficult). We used to teach Pre-Calc using the CPM and it worked pretty well with students who were in their fourth year in the system, but I did discover that when we went to a traditional text for PC, the Calc students were stronger in equation solving than my previous calculus students. Less knowledge of the concepts of limits, slope, and area, but better equation solving, which to me was a plus. So there was a tradeoff there and I probably wouldn’t go back to CPM PC.
4) Every lesson in CPM is supposed to have a wrap up in which you discuss the concepts discovered during the lesson. There are also Toolkit Notes in which you record formulas, etc. If teachers skip the wrap up, then you are correct that the students will be left not understanding the purpose of the lesson. Learning Targets are also helpful, in which I post on the board the ideas that we are exploring and then touch back on those LTs at the end, as well as referring to them while the students are working.
5) Practice and homework is definitely a weakness. I agree that students definitely don’t get enough practice and we supplement the curricula with extra practice worksheets on a regular basis. Due to our weird school schedule we have short periods on Friday and so typically Friday is a wrap up/extra practice day. The worksheets are typical “do lots of problems” exercises.
I am skeptical of anything called “education research” because it generally seems unscientific. There are never control groups, you can’t conduct blind studies, etc. Comparing one school to another, each using a different curriculum generally fails to take into account differences in the school populations or differences in teachers. So any evaluation would, except in the extreme, be based on anecdotal observations. My observation of this curriculum is that students are engaged in their learning; that even students who struggle more do better once they are engaged; and that students enjoy themselves in my math classes. I have even had reports from other teachers that my class is chosen as “my favorite” by a fair number of students. Who can say that in a high school math class? 😁 Even students who have struggled in math have been able to contribute to the group discussions. I change up the groups every chapter so no one is stuck with a group that struggles to either work together or come up with good answers to problems. I have found their engagement to be much better than when they were seated in rows being fed concepts. There are challenges but what it boils down to, in my opinion, is that a good teacher will make the CPM curriculum interesting and when the students are interested, they learn more.
Where I am seeing serious problems is the mainstreaming of Special Ed and non-English speaking students. Asking students to discuss basic problems as a group and come up with good progress is all well and good, but insert a student who speaks minimal English or a student with an IEP and no paraeducator support, and now we are asking the students to deal with issues far beyond their capabilities. They might be able to communicate with those students but to discuss mathematical issues beyond the abilities of those students is not something they are trained for or should be expected to do.
Anyway, there’s a few thoughts from the other side of the aisle.
LikeLike
Thanks for your detailed remarks! I actually agree with many of the points you make, so no need for separating people across “aisles” 😁! Will have to respond at greater length later though.
LikeLike
In response to Heresolong, I agree with several of your points above except number 1 and will respond to each:
1) I think almost everyone knows what the Socratic method is, and I agree that it is a good way to teach at times. However, if you read up on the Socratic method you will also learn that Plato believed we already had knowledge inside us, “in our souls,” and the Socratic method was designed to draw out of us what we already knew. While I do not want to digress into the details of Platonic philosophy, comment 1 is missing the main point. The quote was simply an expression of extreme frustration by a student who was not understanding the material (nor were her friends) and who felt that the teacher was not providing adequate assistance because of stubborn adherence to a single teaching method. In most lines of work this would be taken as a BIG red flag that something is wrong with the method at least in the instance at hand. In the case of CPM orthodoxy it is defended as a virtue. I believe that *good* teachers always have to remain flexible and try a different means of communication if the first attempt is not working.
This comment also came from a student in the original CPM Precalculus textbook trial at Aragon high school which corroborates Heresolong’s point #3 above, stating “This is not a good curriculum to start in a higher level class.” By that level of mathematical complexity, I still believe that CPM is less effective than in easier topics like Algebra 1, and possibly geometry and Algebra 2, as Heresolong also alludes to in comment 3. More on this concern follows.
2) I agree that CPM can be used successfully in the easier math classes as noted above and several places in the main article as long as the class is reasonably well-behaved and not handicapped as Heresolong also notes in his second to last paragraph. Two quotes from the original article again:
"Many teachers have told me that students are more engaged with the CPM math curriculum than with any other series that they have tried. Students have active discussions about the material and work on group problems in class versus passively listening to lectures, taking notes, and only working actively when they do homework alone after school.
As long as the program works in this manner this is definitely a strong positive in its favor. Mathematics is definitely learned by working problems actively rather than watching a teacher do them on the board. It is also a major plus to work problems in class, when others are around to offer a helping hand, instead of finding later, when starting the homework at home alone, that one didn’t understand the material."
and
"As I have found with many ideas in education, such theories work great when one has motivated students who actually do the work. If the student groups are well-structured, the better students help those in their group who struggle with math, and everyone benefits. The good students benefit because, paradoxically, there is no better way to learn a subject than to teach it. The less mathematically-inclined students get help from their peers, which is often less intimidating than asking a question from the teacher.
However, if a teacher has a class of mainly lower level students who have not done well in math previously, the CPM method can become problematic. Putting pre-teens or teens who “hate math” into groups results in a major “classroom management” challenge for a teacher. The group conversation is often on any popular teenage topic other than mathematics when the teacher is not watching!"
3, 4, and 5 ) I agree with the points made by Heresolong in 3 to 5 above with the caveats about CPM use in higher level math as Heresolong also notes in 3.
I also **strongly encourage** readers to carefully reread the article section entitled "Critique of the Self-discovery Methodology" which details my concerns about self-discovery teaching in more advanced mathematical topics. Sometimes when one writes a longer article on a complex subject, reader attention flags and later points are not noticed or are unfortunately skipped completely.
LikeLike